본 글은 참고문헌 [2]를 참고하여 작성했음을 알립니다.
목차
- 프로펠러 모델링
- DC모터로 근사한 BLDC 모터 모델링
- 전체 추력 시스템 모델링
프로펠러 모델링 [1][2]
회전 축 방향으로 상대풍 $V_{\infty}$이 불어오는 회전 속도 $\omega_{\text{prop}} [rad/s]$, 프로펠러 직경 $D$을 가지는 프로펠러를 상사법칙(Law of Similarity)에 따라 다음과 같이 추력과 토크가 발생한다고 모델링한다. $\rho$는 공기밀도, 상사법칙에 따라 무차원화된 계수, $k_T$는 추력 계수, $k_Q$는 토크 계수, $k_P = 2\pi k_Q$는 동력 계수이다.
회전 속도 $n=\omega_{\text{prop}} \frac{1}{2\pi} [rev/s]$
전진비 Advanced ratio $J=\frac{V_{\infty}}{nD}$
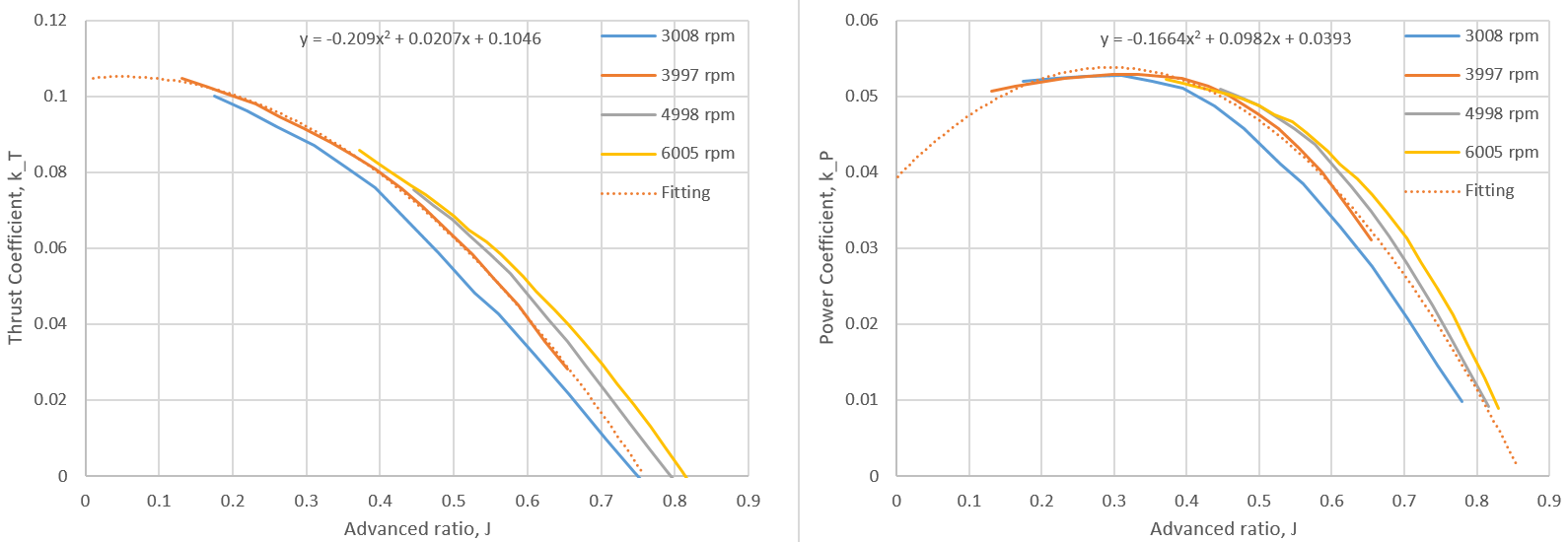
$$T_{\text{prop}} = k_T \rho n^2 D^4, \hspace{5mm} k_T = f_n (J)$$
$$Q_{\text{prop}} = k_Q \rho n^2 D^5, \hspace{5mm} k_Q = f_n (J) $$
일반적으로 프로펠러의 추력 계수 $k_T$와 토크 계수 $k_Q$는 전진비 $J$에 대한 2차 다항식 함수로 피팅한다. 예를 들어 Master Airscrew사의 11x8 프로펠러의 추력 계수 $k_T$ 와 동력 계수 $k_P$를 보면 다음과 같다.

DC모터로 근사한 BLDC 모터 모델링[2]
모터의 회전 속도 $w_{\text{motor}}$는 감속비 $\beta$를 가지는 감속기어를 물린다면 프로펠러의 회전속도 $\omega_{\text{prop}}$는 다음의 관계를 가진다.
$\omega_{\text{motor}} = \beta \omega_{\text{prop}}$
$V_{\text{in}} = V_{\text{ref}} u_{\text{in}}, \hspace{5mm} 0\leq u_{\text{in}} \leq 1$
배터리-모터 폐회로는 RLC 회로 구조로, 키르히호프의 전압법칙을 만족한다. $i$는 회로에 흐르는 전류, $i_0$는 무부하 전류, $R$는 모터의 저항, $K_{\text{bemf}}$는 Lenz의 법칙에 따라 DC모터의 회전에 의한 역기전력(Back EMF) 계수이다.
$$V_{\text{in}} = i R + K_{\text{bemf}} \omega_{\text{motor}} +L \frac{di}{dt}$$
정상상태를 가정하면 전류의 변화율 항이 소거된다.
$$V_{\text{in}} = i R + K_{\text{bemf}} \omega_{\text{motor}}$$
모터가 낼 수 있는 토크 $Q_{\text{motor}}$는 흐르는 전류량에 비례한다. $k_{Q_m}$는 모터의 토크 상수이다.
$$Q_{\text{motor}} = k_{Q_m} \left(i-i_0 \right)$$
$$Q_{\text{gear}} = \beta Q_{\text{motor}} $$
참고 문헌[2]에 따라, 정상상태를 가정하면 모터의 토크 상수 $k_{Q_m}$와 역기전력 상수$k_{\text{bemf}}$, 모터의 속도 상수 KV는 다음과 같이 근사화 할 수 있다.
$$k_{Q_m} = k_{\text{bemf}} = \frac{1}{KV}$$
모터의 토크 $Q_{\text{motor}}$와 회전하는 프로펠러의 항력으로 인한 토크 $Q_{\text{prop}}$에 의해 프로펠러의 회전속도가 결정된다. $I_{\text{prop}}$은 프로펠러의 관성모멘트이다.
$$\frac{d\omega_{\text{prop}}}{dt} = \frac{1}{I_{\text{prop}}} \left(Q_{\text{gear}} -Q_{\text{prop}}\right) = \frac{1}{I_{\text{prop}}} \left(\beta Q_{\text{motor}} -Q_{\text{prop}}\right)$$
Turnigy 사의 BLDC 모터 Aerodrive SK3 5045 550kv outrunner motor를 보면 모터의 특성은 500KV, 내부 저항 0.022 Ohm, 무부하 전류 정보는 없고 전압 범위는 Li-po 배터리 기준 5~7S을 사용하고 최대 전류 60A, 최대 전력 1350W를 사용할 수 있다.
Turnigy 사의 BLDC 모터 Aerodrive SK3 3548 840kv outrunner motor를 보면 모터의 특성은 840KV, 내부 저항 정보는 없고, 무부하 전류는 0.016A, 전압 범위는 Li-pi 배터리 기준 3~4S을 사용하고 최대 전류 50A, 최대 전력 656W를 사용할 수 있다.
이 정보를 바탕으로 무부하 전류가 매우 적다고 가정하면 Aerodrive SK3 5045 550kv 모터 모델링 파라미터는 다음과 같이 결정할 수 있다.[2]
$i_0 \approx 0$
$k_{Q_m} =k_{\text{bemf}} \approx 0.0018182$$
다음 포스팅은 전개한 프로펠러-모터 모델의 파라미터를 이용하여 Gazebo의 모터 모델링 파라미터에 대입할 수 있도록 식을 유도하고자 한다.
Reference
[1] J.B. Brandt, R.W. Deters, G.K. Ananda, O.D. Dantsker, and M.S. Selig, UIUC Propeller Database, Vols 1-3, University of Illinois at Urbana-Champaign, retrieved from https://m-selig.ae.illinois.edu/props/propDB.html.
[2] 변희재, 전기 동력 무인항공기의 추력 시스템 모델링 및 제어, 석사학위논문, 한국항공대학교, 2016.