IMU 란?
IMU는 Inertial Measurement Unit으로 관성 측정 장치라 부르고, 가속도계와 각속도계로 구성되어 장치의 자세를 계측하는 센서이다.
가속도계는 장치의 가속도를 계측하는 센서이나, 정확히 말하면 비력(Specific Force)를 측정한다. 이는 물체가 받고 있는 힘에서 중력을 뺀 가속도를 계측한다는 것이다.
계측되는 가속도를 $a_m$, 물체의 질량을 $m$, 중력을 포함하여 물체에 가해지는 힘을 $F$, 중력을 $F_g$라 하면 3축 가속도 모델은 다음과 같다.
$$a_m = \frac{1}{m} \left( F - F_{g} \right) $$
항법 좌표계 상에서 표현하는 중력은 다음과 같다. (일반적으로 NED 좌표계라고 부르는..)
$$F_g = \left[ \matrix{0 \\ 0 \\ mg} \right] $$
그래서 지면에 고정된 상황과 자유 낙하 상황에서의 계측되는 가속도는 다음과 같다.
$$a_{m,fixed} = \frac{-F_g}{m} \hspace{10mm} a_{m,free-fall} = 0$$
자세의 계측 방법 1 - 고정된 상태에서 가속도 벡터 기반으로 자세 역산
중력 가속도 값을 알고(대략 9.80665 m/s2) 중력 이외의 가속도가 가해지지 않는다고(지면에 고정된) 가정하면, 센서의 프레임에 대해서 가속도 벡터를 이용하면 자세를 계측할 수 있다.
동체 축 좌표계(Body Frame)에서 표현하는 중력은 다음과 같다. 여기서 위첨차는 요소가 표현된 프레임(B : 동체 축 좌표계, N : 항법 좌표계) 이며, 아래첨자는 출발한 좌표계이다. 그래서 $C_N^B$ 는 항법 좌표계(N)에서 동체 축 좌표계(B)으로의 방항 코사인 행렬(DCM)이다.
$$F_g^B = C_N^B \left[ \matrix{0 \\ 0 \\ mg} \right]^N = mg \left[ \matrix{ -\text{sin} \theta \\ \text{sin} \phi \text{cos} \theta \\ \text{cos} \phi \text{cos} \theta } \right]^B $$
$$a_m = g \left[ \matrix{\text{sin} \theta \\ - \text{sin} \phi \text{cos} \theta \\ - \text{cos} \phi \text{cos} \theta } \right]$$
위 식의 가속도 성분으로부터, 롤 각과 피치 각을 역산 할 수 있다.
$$\theta_{acc} = \text{sin}^{-1} \left( \frac{a_{mx} }{g} \right)$$
$$\phi_{acc} = \text{tan}^{-1} \left( \frac{a_{my}}{a_{mz}} \right) $$
위 방식으로 자세를 계산하는 방법은 빠르고 간단하지만, 진동이나 외력 등에 의해 그 성능이 영향을 받는다. 심지어 가속도 센서 자체도 고주파 잡음이 상당한 편이다.
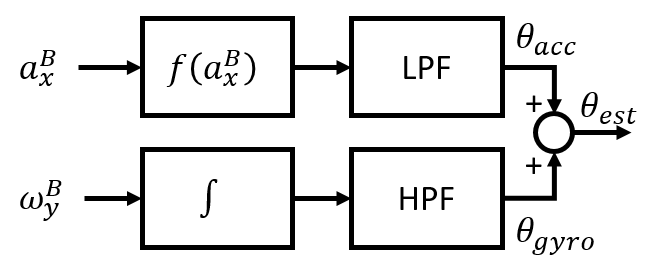
자세의 계측 방법 2 - 가속도계와 각속도계를 이용한 상보필터
가속도계를 이용한 각도 추정은 drift 가 없기 때문에 추정한 자세각이 표류하지 않는다. 그러나 외력이나 잡음에 의해 성능이 영향을 받는다.
각속도계를 이용한 각도 추정은 센서 자체의 bias 나 오차의 누적으로 인해 drift가 발생한다. 시간이 지남에 따라서 어떤 방향으로 값이 흐르는 것이다. 따라서 짧은 순간의 동적인 계측에서는 괜찮은 성능이지만 오래 쓸 것은 아니다.
위와 같이 사용 장치에 대한 각도 추정을 고려했을 때
가속도계로부터 측정한 각도 추정 값은 저주파 영역을(오래 쓰고)
각속도계로부터 측정한 각도 추정 값은 고주파 영역을(단기간 쓰고)
사용해보는 것은 어떨까?
위와 같이 상호보완적으로 구성하는 것을 상보 필터, Complementary Filter라고 부르는 듯 하다.
그래서 주파수 영역에서 표현된 상보필터의 구성은 다음과 같다.
$$\theta_{est} = \text{LPF} \theta_{acc} + \text{HPF} \int \dot{\theta}_{gyro}$$
$$\theta_{est} = \frac{1}{\tau s + 1} \text{tan}^{-1}\left( \frac{a_{mx}}{g} \right) + \frac{\tau s }{\tau s +1} \frac{1}{s} \dot{\theta}_{gyro} $$
일반적으로는 디지털 시스템에서 사용하기 때문에 변환하는 방법은 이 글을 참고한다.
자세의 계측 방법 3 - 지자계 센서를 이용한 진북의 추정
이는 위 글을 참조하자.
자세의 계측 방법 4 - 칼만 필터를 이용한 자세 추정
칼만 필터는 시스템 모델을 이미 알고있는 상태에서 모델의 상태를 예측하고 추정하는 과정을 통해서 상태를 추정한다.
칼만 필터의 종류는 다양하며 다음과 같이 정리해볼 수 있다.
선형 칼만 필터(LKF, Linear Kalman Filter)는 가장 간단한 칼만 필터이며, 선형 시스템 모델을 사용한다.
확장 칼만 필터(EKF, Extended Kalman Filter)는 예측 과정에서 비선형 시스템 모델을 그대로 사용하기에 비선형 모델에 대해서 적용 가능하다는 장점이 있다. 다만 칼만 이득 계산에서 매번 시스템 모델 선형화를 진행한다.
적응 칼만 필터(Adaptive Kalman Filter)는 앞서 LKF, EKF가 예측/추정 과정에서 사용하는 고정된 시스템/계측 잡음 공분산 행렬(System/Measured Noise Covariance Matrix)을 연역 잔차(Priori residual)과 귀납 잔차(Posteriori residual)을 바탕으로 매번 갱신한다. 이 덕에 시스템 잡음이나 계측 잡음을 잘 모른다고 해도 이 또한 추정하기 때문에 최적 추정을 보장하진 못하나 모델 추정의 정확성을 높일 수 있다.
무향 칼만 필터(Unscented Kalman Filter)는 EKF의 선형화로 인한 문제를 무향 변환(Unscented Transformation)으로 대체하여 자코비안을 구할 필요가 없기에 비선형성이 높은 시스템에도 적합하다는 장점이 있다.
칼만필터를 이용한 자세 추정 방법은 다른 글에서 다루도록 한다.
[1] A. Kaviyarasu, "Fundamentals of Attitutde Estimation", Lecture Note.
[2] "AHRS: Attitude and Heading Reference Systems", https://ahrs.readthedocs.io/en/latest/index.html
'개인공부 > 망원경' 카테고리의 다른 글
| 자동 망원경을 위한 아두이노 디스플레이 메뉴 UI 설계 (0) | 2022.12.31 |
|---|---|
| [작성중] 지자기 센서로부터 자북/진북 방향 얻기 (0) | 2022.12.25 |
| 적도의 식 망원경 자동화를 위한 조사 (2) | 2022.12.20 |
| [Arduino] NodeMCU v3 으로 기능 개발하기 (1) (0) | 2022.12.18 |
| 레이저 콜리메이터를 이용한 뉴턴식 반사망원경의 광축 정렬 (How to collimate a telescope using laser collimator?) (2) | 2022.12.10 |