다음의 조건을 가지는 지구 궤도 위성에 대해, 시간에 따른 운동을 모의한다.
근지점 반경 perigee radius $r_p=9,600 \text{km}$
원지점 반경 apogee radius $r_a=21,000 \text{km}$
상수 $\mu=398,600$
궤도 운동에 대한 변수 계산하기
이심률 Eccentricity $e$
$$e=\frac{r_a - r_p}{r_a + r_p} = 0.3725 $$
각운동량 Angular momentum $h$은 perigee 조건으로부터 계산하면
$$h = \sqrt{r_p \mu \left(1 + e\right) }= 72,472 \text{km2/s}\leftarrow r=\frac{h^2}{\mu} \frac{1}{1 + e \text{cos}\theta}$$
공전 주기 $T$
$$T=\frac{2 \pi}{\mu^2} \left( \frac{h}{\sqrt{1-e^2}} \right)^3 = 18,834 \text{sec} = 5.23 \text{hrs}$$
시간에 따른 이각 계산하기
정의는 다음과 같다.
- $\theta$ : True anomaly, 진 근점 이각
- $M_e$ : Mean anomaly, 평균 근점 이각
- $E$ : Eccentric anomaly, 편심 이각
시간에 대한 관계로 인해, $t \rightarrow M_e \rightarrow E \rightarrow \theta$ 순서대로 계산해야한다.
평균 근점 이각 $M_e$와 시간 $t$에 대한 관계는 다음과 같다.
$$M_e = \frac{\mu^2}{h^3} \left(1-e^2 \right)^{3/2} t = \frac{2\pi}{T}t$$
평균 근점 이각 $M_e$와 편심 이각 $E$의 관계는 다음과 같다. 이를 케플러 방정식이라 부른다.
$$M_e = E-e\text{sin} E$$
편심 이각 $E$와 진 근점 이각 $\theta$간의 관계는 다음과 같다.
$$\frac{E}{2} = \sqrt{\frac{1-e}{1+e}} \text{tan}\frac{\theta}{2}$$
$$\theta = 2 \text{tan}^{-1}\left( \sqrt{\frac{1+e}{1-e}} \text{tan} \frac{E}{2} \right)$$
진 근점 이각으로부터 상태량 계산하기
초점으로부터의 거리 $r$
$$r= \frac{h^2}{\mu} \frac{1}{1+e \text{cos}\theta }$$
시선 속도 Radial velocity $v_r$
$$v_r = \frac{\mu}{h} e \text{sin}\theta$$
횡속도 Transverse velocity $v_{\perp}$
$$v_r = \frac{\mu}{h} \left(1+ e \text{cos}\theta \right)$$
MATLAB으로 구현하기
위의 정리대로 구현한 코드는 다음과 같다.
참고로 평균 근점 이각과 진 근점 이각은 vpasolve()을 통해서 수치 계산을 했다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
%% Basic Parameters
ra = 21000;
rp = 9600;
mu = 398600;
e = (ra - rp)/(ra + rp);
h = sqrt(rp * mu * (1 + e * cos(0)));
T = (2 * pi / power(mu,2)) * power(h/sqrt(1-e*e),3);
fprintf("GM \t:%10.2f km2/sec \n",mu);
fprintf("Semi-major\t:%10.2f km \n",ra);
fprintf("Semi-minor\t:%10.2f km \n",rp);
fprintf("Period \t:%10.2f sec \n",T);
%% Calculate states
syms Eval;
for i = 0 : 200 : floor(2*T)
t = i;
% Anomaly as a function of time
Me = warp_2pi(2 * pi * t / T);
E = double(vpasolve((Eval - e * sin(Eval)) - Me, Eval));
theta = 2 * atan(sqrt((1+e)/(1-e))*tan(E/2));
fprintf("T %6.2f s : E %6.1fD / t %6.1f D \n",t, E*57.296,theta*57.296);
% Properties from true anomaly
r = (h*h/mu)/(1+e*cos(theta));
r_vec = [ra * (cos(theta) - e), rp * sin(theta)];
ur_vec = r_vec/norm(r_vec);
vr = (mu/h)*e*sin(theta); % Radial component of velocity
vt = (mu/h)*(1+e*cos(theta)); % Transverse component of velocity
v = norm([vr vt]);
vr_vec = vr * ur_vec;
vt_vec = vt * [-ur_vec(2) ur_vec(1)];
v_vec = vr_vec + vt_vec;
% Show me
figure(1);
angles = [0:10:360];
plot([ ra*e],[0],'or'); hold on; grid on; % Focus points
plot([-ra*e],[0],'ok'); % Focus points
plot(ra,0,'kx');
plot(0,rp,'kx');
plot(ra * cosd(angles), rp * sind(angles),'--r'); % Main Path
plot(ra * cosd(angles), ra * sind(angles),':k'); % Mean Circle
plot(ra * cos(theta), rp * sin(theta),'xr'); % Point
plot(ra * cos(theta)+[0, vr_vec(1)]*1000.0,...
rp * sin(theta)+[0, vr_vec(2)]*1000.0,'m'); % Vr
plot(ra * cos(theta)+[0, vt_vec(1)]*1000.0,...
rp * sin(theta)+[0, vt_vec(2)]*1000.0,'m'); % Vt
plot(ra * cos(theta)+[0, v_vec(1)]*1000.0,...
rp * sin(theta)+[0, v_vec(2)]*1000.0,'b'); % Velocity Vector
plot([ra*e, ra * cos(theta)], [0 rp * sin(theta)],':r');
text(ra*0.7, rp*2.3,'R_p 9.6 E3 km');
text(ra*0.7, rp*2.0,'R_a 2.1 E4 km');
text(ra*0.7, rp*1.7,'T 5.23 hrs');
text(ra*0.7, rp*1.4,' 18,834 sec' );
title_string = sprintf("Time %6.0f sec : E %7.2f D / t %7.2f D",t, E*57.296, theta*57.296);
title(title_string);
hold off;
% break;
end
|
cs |
Colorscript는 MATLAB을 지원하지 않는다는게 너무 아쉽다.
결과
코드 실행 결과는 다음과 같다. 두 번의 주기를 돌린다.
붉은 대시선은 타원 궤도
까만 원과 빨간 원은 타원 궤도의 초점
마젠타 색 선은 시선 속도와 횡 속도
파란 선은 위성의 속도 벡터
빨간 X는 위성의 위치이다.
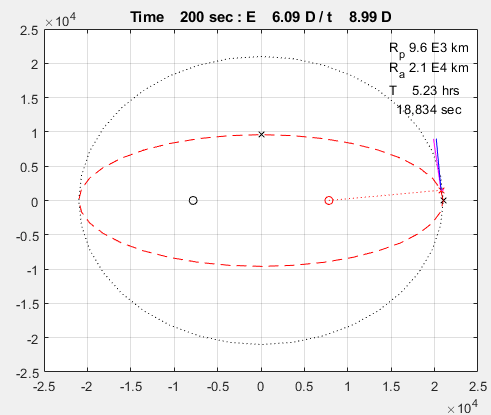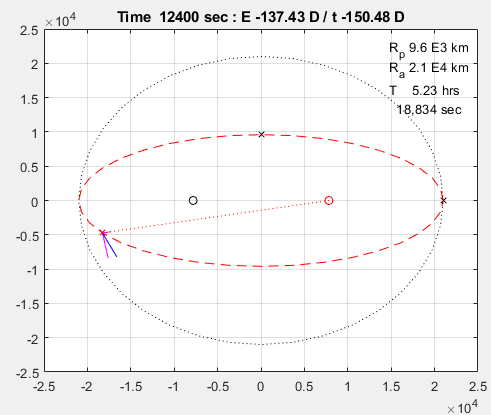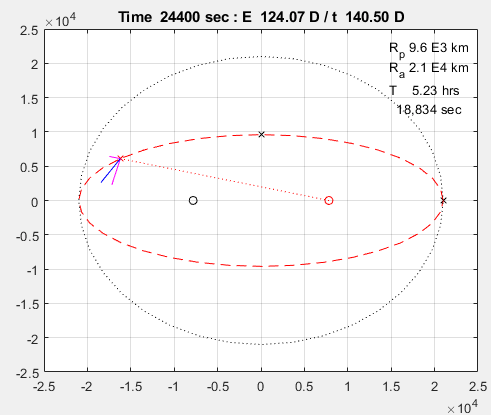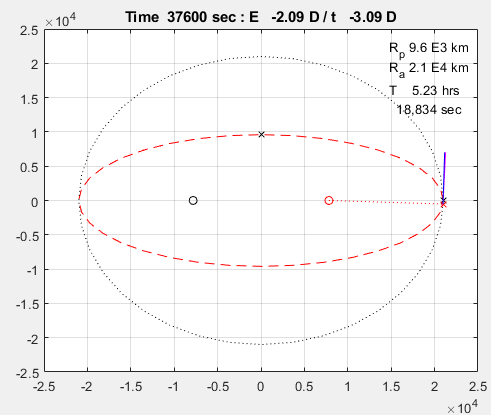
끝.
'개인공부 > 궤도역학' 카테고리의 다른 글
| 태양 주위의 가관측한 행성의 궤도 (0) | 2023.03.28 |
|---|---|
| Orbital Mechanics, Ch.8.10 행성의 천체력 계산 (0) | 2023.03.12 |
| Orbital Mechanics, Ch.5 Preliminary Orbit Determination (0) | 2023.02.19 |
| 궤도 계산 2D - 2 : 태양-지구 궤도 (0) | 2023.02.19 |
| Orbital Mechanics, Ch.4 Orbits in Three Dimensions (0) | 2023.02.14 |